1582 - Special Positions in a Binary Matrix
problem
Given an m x n binary matrix mat, return the number of special positions in mat.
A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).
Example 1:
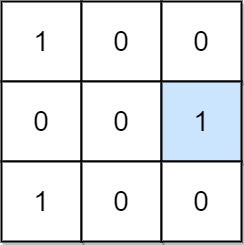
Input: mat = [[1,0,0],[0,0,1],[1,0,0]] Output: 1 Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.
Example 2:
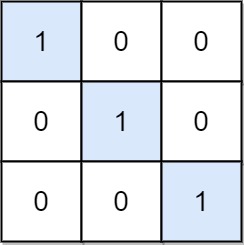
Input: mat = [[1,0,0],[0,1,0],[0,0,1]] Output: 3 Explanation: (0, 0), (1, 1) and (2, 2) are special positions.
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 100mat[i][j]is either0or1.
submission
// too lazy for anything clever, just brute force
// also 1 line for fun
impl Solution {
pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {
mat.iter()
.enumerate()
.flat_map(|(i, row)| {
std::iter::repeat(i).zip(row.iter().enumerate())
})
.filter(|&(i, (j, &v))| {
v == 1
&& mat[i].iter().sum::<i32>() == 1
&& mat.iter().map(|r| r[j]).sum::<i32>() == 1
})
.count() as _
}
}