1642 - Water Bottles
description
There are numBottles water bottles that are initially full of water. You can exchange numExchange empty water bottles from the market with one full water bottle.
The operation of drinking a full water bottle turns it into an empty bottle.
Given the two integers numBottles and numExchange, return the maximum number of water bottles you can drink.
Example 1:
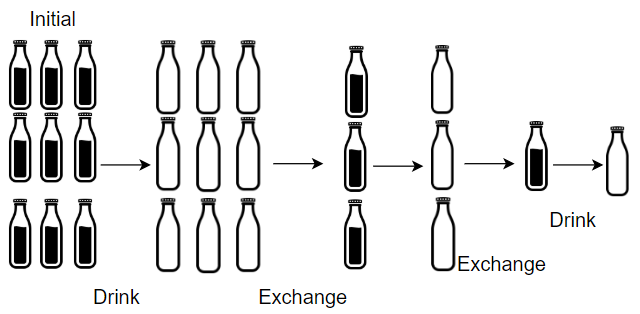
Input: numBottles = 9, numExchange = 3 Output: 13 Explanation: You can exchange 3 empty bottles to get 1 full water bottle. Number of water bottles you can drink: 9 + 3 + 1 = 13.
Example 2:
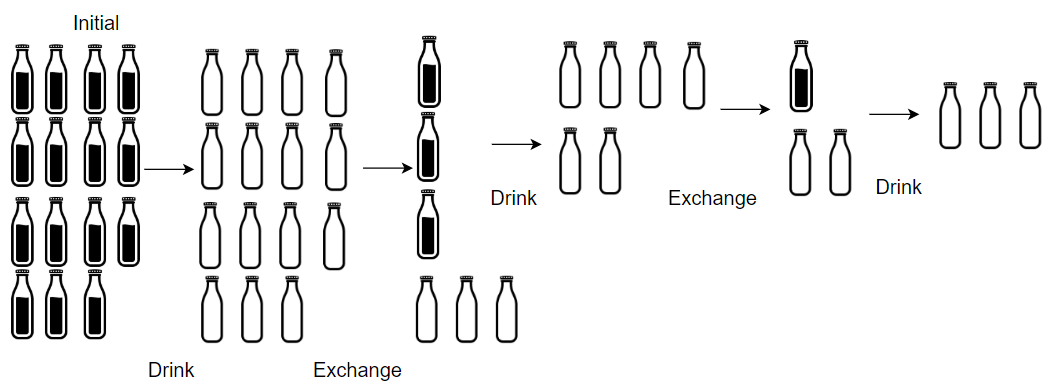
Input: numBottles = 15, numExchange = 4 Output: 19 Explanation: You can exchange 4 empty bottles to get 1 full water bottle. Number of water bottles you can drink: 15 + 3 + 1 = 19.
Constraints:
1 <= numBottles <= 1002 <= numExchange <= 100
submission
impl Solution {
// we could solve this by simulate and it is absolutely ok
// however this is a much clever solution
// think a full bottle as 1 bottle + 1 water
// we exchange k bottle to 1 bottle + 1 water
// effectively we have: (k - 1) bottle = 1 water
// after the process, we'll have at least 1 bottle
// initially we have n water and n bottle, so
// we have: n + floor((n - 1) / (k - 1))
pub fn num_water_bottles(n: i32, k: i32) -> i32 {
n + (n - 1) / (k - 1)
}
}