3100 - Water Bottles II
problem
You are given two integers numBottles and numExchange.
numBottles represents the number of full water bottles that you initially have. In one operation, you can perform one of the following operations:
- Drink any number of full water bottles turning them into empty bottles.
- Exchange
numExchangeempty bottles with one full water bottle. Then, increasenumExchangeby one.
Note that you cannot exchange multiple batches of empty bottles for the same value of numExchange. For example, if numBottles == 3 and numExchange == 1, you cannot exchange 3 empty water bottles for 3 full bottles.
Return the maximum number of water bottles you can drink.
Example 1:
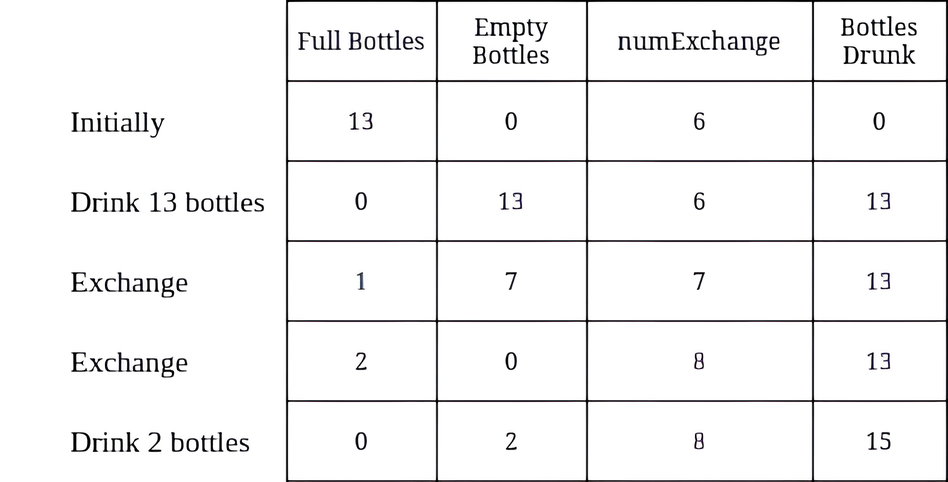
Input: numBottles = 13, numExchange = 6 Output: 15 Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.
Example 2:
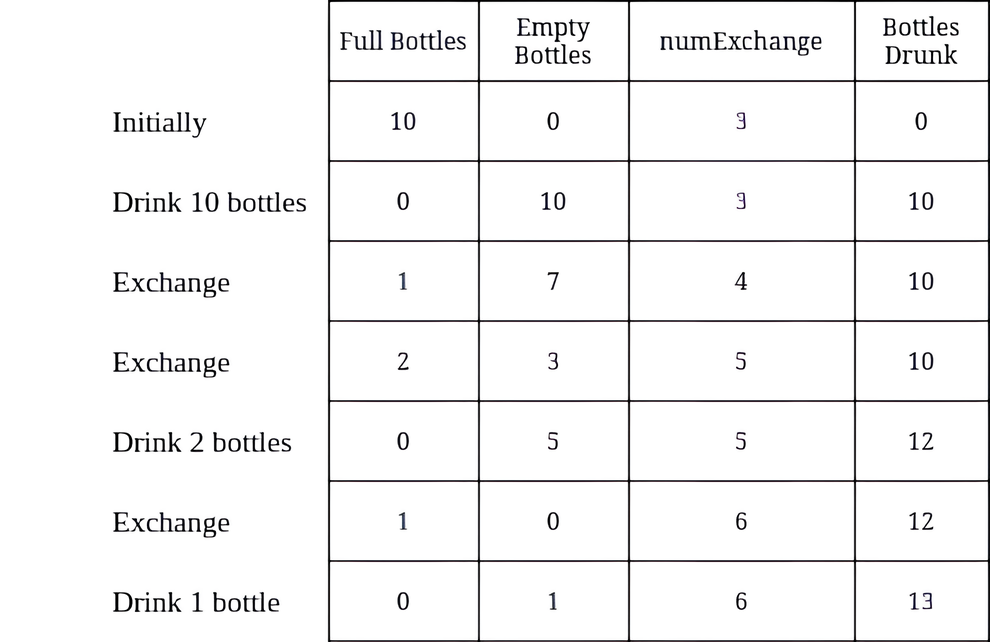
Input: numBottles = 10, numExchange = 3 Output: 13 Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.
Constraints:
1 <= numBottles <= 1001 <= numExchange <= 100
submission
impl Solution {
// just simulate, exchange and drink it immediately
pub fn max_bottles_drunk(
mut num_bottles: i32,
mut num_exchange: i32,
) -> i32 {
let mut drinks = num_bottles;
while num_bottles >= num_exchange {
// exchange and drink
num_bottles -= num_exchange - 1;
drinks += 1;
// raise exchange price
num_exchange += 1;
}
drinks
}
}