Leetcode刷题笔记 4
本周Leetcode刷题笔记
309. Best Time to Buy and Sell Stock with Cooldown🔗
You are given an array prices where prices[i] is the price of a given stock on the ith day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
- After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
因为这个问题规模不大,因此可以通过比较naive的DP来做,假设dp[i]是到第i步时在我们卖出股票的前提下,赚到的最多的钱。那么我们可以遍历前面的[0, i-1]区间内的步骤,来更新最大值。代码如下
int maxProfit(vector<int>& prices) {
unordered_map<int, int> dp;
int res = 0;
for (int i = 1; i < prices.size(); i++) {
for (int j = 0; j < i; j++) {
dp[i] = max(dp[i], dp[j - 2] + max(prices[i] - prices[j], 0));
}
dp[i] = max(dp[i], dp[i-1]);
res = max(res, dp[i]);
}
return res;
}
这个代码挺难理解的,写的比较差,复杂度也是o(n^2)的,实际上这个题目有更好的o(n)解法。以状态机的方式来思考,我们一共可能有三种状态:
- s0 空闲状态,此时我们可以买入,也可以跳过下一次交易时间。买入则进入s1,跳过则保持在s0
- s1 刚刚买入,此时可以跳过下一次交易时间也可以卖出。跳过下一次交易则我们保持在s1,卖出则进入s2
- s2 刚刚卖出,此时只能跳过下一次交易时间。跳过后我们进入s0
我们可以看到,不同的状态有不同的进入方式,假如我们每一步都维持每个状态的最大值,那么最终我们需要的最大值就在s0和s2之间,因为s1刚刚买入显然不会是最大值。初始状态则如下:s0是空闲状态,因此是0,s1刚刚买入,所以初始值是-prices[0],s2刚刚卖出其实是不可能出现的,我们将其初始化为最小值,防止影响我们的结果。同时这里其实也不需要使用vector存储状态,不过我这里就不改了。
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
vector<int> s0(prices.size(), 0);
vector<int> s1(prices.size(), 0);
vector<int> s2(prices.size(), 0);
s1[0] = -prices[0];
s0[0] = 0;
s2[0] = INT_MIN;
for (int i = 1; i < prices.size(); i++) {
s0[i] = max(s0[i - 1], s2[i - 1]);
s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]);
s2[i] = s1[i - 1] + prices[i];
}
return max(s0[prices.size() - 1], s2[prices.size() - 1]);
}
95. Unique Binary Search Tree II🔗
Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.
这个题要求返回由[1, n]区间内所有的数字构成的全部平衡二叉树。一般这种题我的第一反应只会是递归,思路也比较清晰,从[1,n]区间选一个数i作为根节点的值,再构造由[1, i-1]和[i+1, n]构成的平衡二叉树,作为根节点的左右节点。相比于使用[l, r]作为区间范围,我更偏向于使用由n和base表示的[1+base, n+base]区间范围,因为这样我可以在函数原型内加入一个默认形参,从而免去了另写一个helper函数的麻烦。代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
vector<TreeNode*> generateTrees(int n, int base = 0) {
vector<TreeNode*> ans;
if (n == 0) {
return ans;
}
if (n == 1) {
ans.push_back(new TreeNode(n + base));
return ans;
}
for (int i = 1; i <= n; i++) {
auto vec1 = generateTrees(i - 1, base);
auto vec2 = generateTrees(n - i, i + base);
if (vec1.empty() && vec2.empty()) {
ans.push_back(new TreeNode(i + base));
} else if (vec1.empty()) {
for (auto right : vec2) {
ans.push_back(new TreeNode(i + base, nullptr, right));
}
} else if (vec2.empty()) {
for (auto left : vec1) {
ans.push_back(new TreeNode(i + base, left, nullptr));
}
} else {
for (auto left : vec1) {
for (auto right : vec2) {
ans.push_back(new TreeNode(i + base, left, right));
}
}
}
}
return ans;
}
但是这边写的还是比较麻烦,其实主要原因出在当n=0时的返回值上,我返回了空集,因此需要做一些复杂的检查和处理。但是如果返回的是一个包含nullptr的集合,则根本不需要写这么复杂。另外这边需要注意的是,我们直接把返回的节点接入根节点上,在实际中会有严重的内存问题,但如果仅仅考虑通过这个问题,则无所谓。如下所示:
vector<TreeNode*> generateTrees(int n, int base = 0) {
vector<TreeNode*> ans;
if (n == 0) {
return { nullptr };
}
for (int i = 1; i <= n; i++) {
for (auto left : generateTrees(i - 1, base)) {
for (auto right : generateTrees(n - i, i + base)) {
ans.push_back(new TreeNode(i + base, left, right));
}
}
}
return ans;
}
1314. Matrix Block Sum🔗
Given a m x n matrix mat and an integer k, return a matrix answer where each answer[i][j] is the sum of all elements mat[r][c] for:
i - k <= r <= i + k,j - k <= c <= j + k, and(r, c)is a valid position in the matrix.
这个问题相对来说比较简单,用前缀和的思路即可,不多说。
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> preSum(m + 1, vector<int>(n + 1, 0));
vector<vector<int>> ans(m, vector<int>(n, 0));
for (int i = 1; i < preSum.size(); i++) {
for (int j = 1; j < preSum[i].size(); j++) {
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
for (int i = 0; i < ans.size(); i++) {
for (int j = 0; j < ans[i].size(); j++) {
int x1 = max(0, i - k), y1 = max(0, j - k);
int x2 = min(m, i + k + 1), y2 = min(n, j + k + 1);
ans[i][j] = preSum[x2][y2] - preSum[x1][y2] - preSum[x2][y1] + preSum[x1][y1];
}
}
return ans;
}
50. Power(x, n)🔗
Implement pow(x, n), which calculates x raised to the power n (i.e., $x^n$).
实现Power(x, n),这个问题n范围比较大,需要使用快速幂算法,同时需要考虑n为0或者为负的情况。注意好这些细节就不算难写。
double myPow(double x, int n) {
if (n == 0) {
return 1.0;
}
if (n == 1) {
return x;
}
bool neg = n < 0;
n = abs(n);
double tmp = myPow(x, n / 2);
tmp = tmp * tmp * myPow(x, n % 2);
return neg ? 1.0 / tmp : tmp;
}
1848. Minimum Distance to the Target Element🔗
Given an integer array nums (0-indexed) and two integers target and start, find an index i such that nums[i] == target and abs(i - start) is minimized. Note that abs(x) is the absolute value of x.
Return abs(i - start).
It is guaranteed that target exists in nums.
简单题,朝两个方向遍历即可。
int getMinDistance(vector<int>& nums, int target, int start) {
for (int i = 0; start + i < nums.size() || start - i >= 0; i++) {
if (start + i < nums.size() && nums[start + i] == target || start - i >= 0 && nums[start - i] == target) {
return i;
}
}
return -1;
}
1704. Determine if String Halves are Alike🔗
You are given a string s of even length. Split this string into two halves of equal lengths, and let a be the first half and b be the second half.
Two strings are alike if they have the same number of vowels ('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'). Notice that s contains uppercase and lowercase letters.
Return true if a and b are alike. Otherwise, return false.
当天的又一个简单题,数前后两半的元音数。
bool isVowel(char c) {
c = tolower(c);
return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u';
}
bool halvesAreAlike(string s) {
int cnt1 = 0, cnt2 = 0;
for (int i = 0; i < s.length() / 2; i++) {
if (isVowel(s[i])) {
cnt1++;
}
if (isVowel(s[s.length() - i - 1])) {
cnt2++;
}
}
return cnt1 == cnt2;
}
735. Asteroid Collision🔗
We are given an array asteroids of integers representing asteroids in a row.
For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). Each asteroid moves at the same speed.
Find out the state of the asteroids after all collisions. If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.
这个题还挺难的,首先我一直没有很好的思路,其次看了别人的思路也没写出自己的代码。这道题其实类似括号匹配,只不过这里匹配之后,需要摧毁其中一个或者全部,剩下的继续参与匹配,因此可以用栈实现。这个题的细节也很重要,什么时候入栈什么时候出栈,绝对值相等时怎么处理,etc,这里贴一段别人的代码。
vector<int> asteroidCollision(vector<int>& asteroids) {
vector<int> ans;
for (int i = 0; i < asteroids.size(); i++) {
if (asteroids[i] > 0 || ans.empty() || ans.back() < 0) {
ans.push_back(asteroids[i]);
} else if (ans.back() <= -asteroids[i]) {
if (ans.back() < -asteroids[i]) {
i--;
}
ans.pop_back();
}
}
return ans;
}
1720. Decode XORed Array🔗
There is a hidden integer array arr that consists of n non-negative integers.
It was encoded into another integer array encoded of length n - 1, such that encoded[i] = arr[i] XOR arr[i + 1]. For example, if arr = [1,0,2,1], then encoded = [1,2,3].
You are given the encoded array. You are also given an integer first, that is the first element of arr, i.e. arr[0].
Return the original array arr. It can be proved that the answer exists and is unique.
简单题,利用异或的性质(A = B ^ C => B = A ^ C)即可,即使不知道性质,也可以在纸上推一推,总之比较简单。
vector<int> decode(vector<int>& encoded, int first) {
vector<int> ans(1, first);
for (auto n : encoded) {
ans.push_back(ans.back() ^ n);
}
return ans;
}
31. Next Permutation🔗
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, it must rearrange it as the lowest possible order (i.e., sorted in ascending order).
The replacement must be in place and use only constant extra memory.
日常题的最后一道,实现next permutation,将一个序列变为它的下一个字典序排列。这个题的算法其实比较简单,即使没有接触过,也可以自己推导出来,有点像手动实现+1,假设区间[1,n],算法步骤如下:
- 找到使得[i, n]非严格单调递减的最大下标i
- 反转[i, n]区间,这里反转指逆序
- 如果i等于1,说明整个序列从最大字典序转换到了最小字典序,因此算法结束
- 找到[i, n]区间内第一个大于$A_{i-1}$的数$A_ k$,即upper bound
- 交换$A_ k$和$A_ {i-1}$
整个算法就这5步,写起来也比较简单,我这里是当时实现的两个版本,第一个比较粗糙,第二个经过了一定的优化。这个题主要的作用还是帮我加深了对next permutation的理解,如果要使用这个函数遍历一个序列的全排列,那么必须先对这个序列进行排序。之前有一次机试我实际上就犯错了,不过当时运气好,测试样例很简单因此侥幸通过了。
void helper(vector<int>::iterator first, vector<int>::iterator last) {
auto it = last - 1;
while (it != first && *(it - 1) >= *it) {
it--;
}
sort(it, last);
if (it != first) {
auto k = it - 1;
while (it != last - 1 && *k >= *it) {
it++;
}
swap(*k, *it);
}
}
void helper(vector<int>::iterator first, vector<int>::iterator last) {
auto it = last - 1;
while (it != first && *(it - 1) >= *it) {
it--;
}
reverse(it, last);
if (it != first) {
auto iter = upper_bound(it, last, *(it - 1));
swap(*(it - 1), *iter);
}
}
void nextPermutation(vector<int>& nums) {
helper(nums.begin(), nums.end());
}
然后是本周的双周赛,这次是我第一次参加双周赛,题目也不算很难,做出来三个,如果时间多点其实也可能能做出来第四个,不过无所谓了。
1909. Remove One Element to Make the Array Strictly Increasing🔗
Given a 0-indexed integer array nums, return true if it can be made strictly increasing after removing exactly one element, or false otherwise. If the array is already strictly increasing, return true.
The array nums is strictly increasing if nums[i - 1] < nums[i] for each index (1 <= i < nums.length).
给一个数组,判定该数组是否可以通过仅仅删除一个元素就成为严格单调递增的数组。当时差点怀疑人生,因为这个题看起来好像简单,实则做起来却完全不是这样。但是这个题简单可能简单在数据不大,数组长度10000级别,也就是说o(n^2)的时间复杂度是可以通过的。因此暴力基本是最好的选择了。
bool canBeIncreasing(vector<int>& nums) {
vector<int> vec;
for (int i = 0; i < nums.size(); i++) {
vec.clear();
for (int j = 0; j < nums.size(); j++) {
if (i != j) {
vec.push_back(nums[j]);
}
}
bool flag = true;
for (int j = 1; j < vec.size(); j++) {
if (vec[j-1] >= vec[j]) {
flag = false;
}
}
if (flag) {
return true;
}
}
return false;
}
1910. Remove All Occurrences of a Substring🔗
Given two strings s and part, perform the following operation on s until all occurrences of the substring part are removed:
- Find the leftmost occurrence of the substring part and remove it from s.
Return s after removing all occurrences of part.
A substring is a contiguous sequence of characters in a string.
这道题倒是没有什么好说的,比第一题简单多了,而且数据级别也很小,直接模拟即可。
string removeOccurrences(string s, string part) {
auto it = s.find(part);
while (it != -1) {
s = s.substr(0, it) + s.substr(it + part.length());
it = s.find(part);
}
return s;
}
1911. Maximum Alternating Subsequence Sum🔗
The alternating sum of a 0-indexed array is defined as the sum of the elements at even indices minus the sum of the elements at odd indices.
For example, the alternating sum of [4,2,5,3] is (4 + 5) - (2 + 3) = 4. Given an array nums, return the maximum alternating sum of any subsequence of nums (after reindexing the elements of the subsequence).
A subsequence of an array is a new array generated from the original array by deleting some elements (possibly none) without changing the remaining elements' relative order. For example, [2,7,4] is a subsequence of [4,2,3,7,2,1,4] (the underlined elements), while [2,4,2] is not.
这个题求序列的子序列最大Alternating Sum,Alternating Sum是序列的偶数下标的数总和减去奇数下标的数总和。这个题其实和之前做过的买股票的题类似,而且比那个更简单,只有两种状态:我们还是用买卖股票的例子来说明,买入和卖出都相当于我们选择了一个数加入子序列,但是他们的下标分别为奇数和偶数,我们也可以跳过,此时不选择该数进入子序列。假如和股票的题类比,这里我们的目标是其实是要亏损最大。
- s0,刚买入股票,此时可以跳过或者卖出,跳过保持s0,卖出进入s1
- s1,刚卖出股票,此时可以跳过或者买入,跳过保持s1,卖出进入s0
代码如下:
long long maxAlternatingSum(vector<int>& nums) {
long long s1 = INT_MIN, s2 = 0;
for (int i = 0; i < nums.size(); i++) {
s1 = max(s1, s2 + nums[i]);
s2 = max(s2, s1 - nums[i]);
}
return max(s1, s2);
}
这里其实我不太确定代码的正确性,理论上来说好像有点问题,当时提交的比较急,没有仔细检查,理论上应该先备份s1的值,在更新s2时使用备份的值而不是更新后的s1。但是总之通过了所有的测试样例。
双周赛的最后一题算是考察数据结构的设计,比较复杂,我就不写了。
然后是本周的周赛,本周周赛对我来说还是比较难的,只做出来两道题。
1913. Maximum Product Difference Between Two Pairs🔗
The product difference between two pairs (a, b) and (c, d) is defined as (a * b) - (c * d).
For example, the product difference between (5, 6) and (2, 7) is (5 * 6) - (2 * 7) = 16. Given an integer array nums, choose four distinct indices w, x, y, and z such that the product difference between pairs (nums[w], nums[x]) and (nums[y], nums[z]) is maximized.
Return the maximum such product difference.
老老实实做可能还比较费劲,但是本题不需要考虑负数,因此直接排序选择前两位和后两位比较简单。
int maxProductDifference(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
return nums[n-1] * nums[n-2] - nums[0] * nums[1];
}
1914. Cyclically Rotating a Grid🔗
You are given an m x n integer matrix grid, where m and n are both even integers, and an integer k.
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:
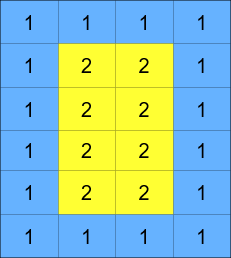
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:
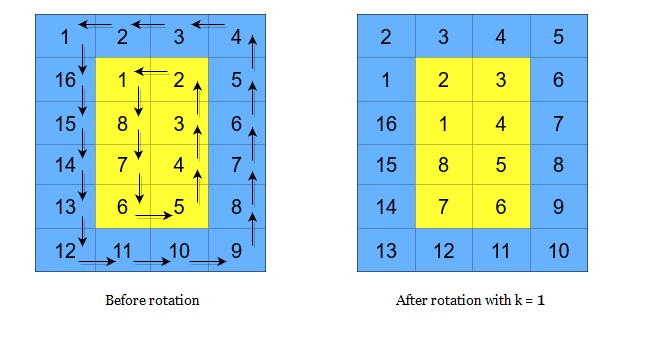
Return the matrix after applying k cyclic rotations to it.
这个题是究级烦,按照规则旋转矩阵的layer,我最后选择的做法是对每一层的坐标都做变换,得到转换前的坐标和转换后的坐标的关系。有多恶心就不提了。
int x1(int j, int a, int b) {
return (0 <= j && j < b) ? 0 : b <= j && j <= a + b - 2 ? j - b + 1 : (a + b - 2 < j && j <= a + b * 2 - 3 ? a - 1 : 2 * a + 2 * b - j - 4);
}
int y1(int j, int a, int b) {
return (0 <= j && j < b) ? j : b <= j && j <= a + b - 2 ? b - 1 : (a + b - 2 < j && j <= a + b * 2 - 3 ? a + 2 * b - j - 3 : 0);
}
vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid.front().size(), l = min(m, n);
vector<vector<int>> ans = grid;
for (int i = 0; i < l / 2; i++) {
int a = m - i * 2, b = n - i * 2, c = a * 2 + b * 2 - 4;
for (int j = 0; j < c; j++) {
int x = i + x1(j, a, b);
int y = i + y1(j, a, b);
int s = i + x1((j + k) % c, a, b), f = i + y1((j + k) % c, a, b);
ans[x][y] = grid[s][f];
}
}
return ans;
}
接下来的两道题我都基本没有思路,可以说是完全不会,连别人的题解都还没理解,就先不写了。这周周赛还是挺惨的,感觉还是基础不行啊,继续加油吧。